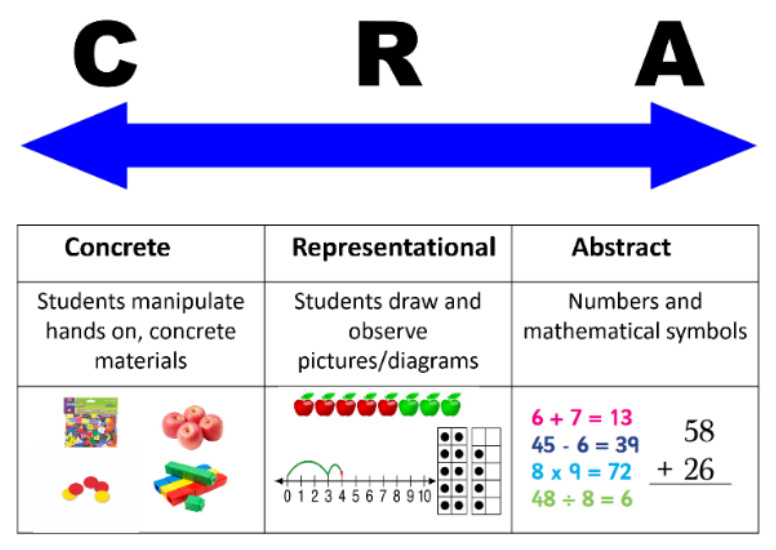
“Hello my fellow Blue Door learners! I hope this month’s message is finding you having a nice start to your summer and of course, staying cool in our brutal Texas heat. I’d like to pick up exactly where I left off in April’s monthly message, which was me sharing one of my secret weapons to teaching our children to have a deep conceptual understanding of mathematics. Following the Concrete to Abstract Continuum is a great start (see model below). “What is it and how is it used?”, you ask. Simply put, it is a tool the breaks down how a learner’s thinking might evolve and progress as they engage in mathematics.
As the model below illustrates, there are three stages. The first stage is the concrete (the ‘doing’ stage), in which children are using objects to solve problems. It brings concepts to life by allowing them to handle physical objects themselves. The second stage is the representational (the ‘seeing’ stage), in which pictures, diagrams and charts are used to represent the objects involved in the math problems. The third stage is the abstract (the ‘symbolic stage’), where children are able to use abstract symbols to model and solve math problems. Once a child has demonstrated that they have a solid understanding of the ‘concrete’ and ‘pictorial’ representations of the problem, the teacher can introduce the more ‘abstract’ concept, such as the mathematical symbols (+,-,×, ÷) to represent addition, subtraction, multiplication, or division.
Although the model below shows the CRA model in a straight line, it is rarely a straight progression for student thinking. In fact, students may move fluidly from one way of representing and understanding to the next depending on the concept and the situation. Even the most abstract thinkers may need to use manipulatives or pictures from time to time, especially when introduced to new concepts and ideas.
Knowing about and following this progression is a great start to building a strong understanding of mathematical concepts. Instead of expecting our young learners to skip to the end goal (the abstract stage), spending the adequate time building their concrete and representational understanding will better prepare them to have a strong conceptual understanding. This will lead them to being better at explaining, justifying, and teaching the math to others around them.
If this information has left you with questions or wanting more explanation, please feel free to reach out to me. Stay tuned for next month, in which I’ll be sharing what having a deeper mathematical understanding looks and sounds like and what we can do to get our young learners there. Until next time!”